The Brain, a User's Manual:
Introducing the
Square of Opposition

By Gabriel Blanchard
With the foundation of predicating laid, we may begin to rear the walls and towers of the Castle Philosophy: syllogisms.
E I, E I O
So! We have gone over how to define words, and how to then use words to take substances and predicate things about them. That covers IA and IB from our introductory outline.
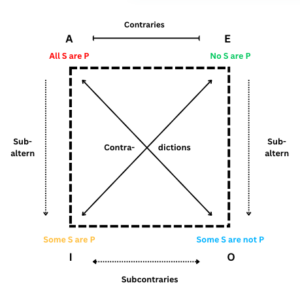
We now proceed to IIA in that outline: the beginning of term logic, starting with the elements from which the square of opposition is constructed. (The square of opposition is a little bit like a calculator for logic—or, really, more like an abacus. In any case, we’ll be coming back to it.) We are still within the Aristotelian realm here, so it may make sense that what we will discuss first are something called categorical propositions. These are statements about what a thing is or is not, or about its attributes, powers, or behaviors, e.g. “Cars are not animals” or “Some Virginians drink tea.”
Categorical propositions can be sorted into different types, based on whether they affirm or deny something, and also on whether they are universal (applying to all members of the group under discussion) or particular (applying to some individual substances, but not necessarily to whole classes of things). Any statement that takes one of the four logically distinct forms below is a categorical proposition—and if you’ve heard expressions like “the difficulty of proving a universal negative,” this classification schema is where those expressions come from:
A. All S are P (universal affirmative)
I. Some S are P (particular affirmative)
E. No S are P (universal negative)
O. Some S are not P (particular negative)1
The phrasing of the E statement occasionally catches people off-guard, since it doesn’t quite match the A statement the same way the O statement matches the I statement. This is because the statement All S are not P, according to English rules of grammar and syntax, is ambiguous; it could mean that no S are P, or merely that not all S are P. (This problem does not always apply in languages other than English, or may apply in some other way.)
"I shall sit down," replied the cat, "but I shall enter an objection with regard to your last. My speeches in no way resemble verbal muck, as you have been pleased to put it ... but rather a sequence of tightly packed syllogisms, the merit of which would be appreciated by such connoisseurs as Sextus Empiricus, Martianus Capella, and, for all I know, Aristotle himself."
"Your king is in check," said Woland.
"Very well, very well," responded the cat, and he began studying the chessboard through his opera glasses.Mikhail Bulgakov, The Master and Margarita
A, I, E, and O statements do not always appear in these obvious forms. Frequently, the verb “are” is replaced with some action or capacity or liking, as in “Some Virginians drink tea”; if we wanted for some reason to be quite pedantic with our phrasing (and pedantry can be a useful way of detecting small errors), we could restate this as “Some Virginians are tea-drinkers.” They can also be obscured in subtler ways—some of which reveal implications these statements have that we might never have thought of alone.
Operation! … -s
There are a few distinct ways we can tinker with our alphabetic assertions here. Three tinkerings in specific are known as the logical operations: namely, conversion, contraposition, and obversion.
1. Conversion
Conversion is the simplest: it just means swapping S and P around, so that No S are P becomes No P are S, etc. However, it can only be validly done with I and E statements. If there is no overlap between S and P in their Venn diagram, then that’s true whichever category we start with, and if there is some overlap between them, the same applies.
With A and O statements, the situation is different. For instance, one category of thing (like cats) can be part of a larger category (like mammals), yet be only one part among others: All cats are mammals does not mean All mammals are cats, because in truth Some mammals are not cats. And we may conveniently use that O statement to show why converting O statements also fails, since Some mammals are not cats indeed, but it does not follow that Some cats are not mammals.
2. Contraposition
Contraposition does two things at once: it swaps the terms S and P, and it negates them both, making them non-S and non-P. Taking our previous example, if All cats are mammals (and they are), then, by contraposition, All non-mammals are non-cats—which is also true. Just like conversion only validly applies to I and E statements, though, you can only validly contrapose A and O statements.
3. Obversion
As everybody knows, you can obvert any categorical proposition, and doing so is a fun trick at parties. Obverting a statement also does two things at once: it changes the statement’s quality from negative to affirmative (or vice-versa), and also negates the predicate (the P term). Accordingly, the obverse forms of the four propositions are as follows:
All S are P ⇒ No S are non-P
Some S are P ⇒ Some S are not non-P
No S are P ⇒ All S are non-P
Some S are not P ⇒ Some S are non-P
We have now laid the groundwork for the square of opposition proper. We won’t get further into that topic until next week’s installment—but go ahead, have a peek at her. She’s gorgeous.
1The letters which give these forms their nicknames (“A statement,” “I statement,” etc.) are a Medieval invention drawn from Latin: its words for “I affirm” and “I deny” are affirmō and nēgō, so the vowels from these words were used to name the statements according to their affirmative or negative quality, using the first vowel for the universal and the second for the particular: affirmō, nēgō. Also, because we have to talk about “A statements” so frequently in this post, we have exchanged our usual “A, B” shorthand denoting “[any sort of thing]” for the “S, P” shorthand observed in formal logic, to avoid tripping the reader up; the S and P come from “substance” and “predicate,” respectively.
A proud uncle to seven nephews, Gabriel Blanchard is CLT’s editor at large. He has a degree in Classics from the University of Maryland, College Park, and lives in Baltmore, MD.
If you enjoyed this piece, be sure to check out Anchored, the official CLT podcast. Thanks for reading the Journal, and have a great day.
Published on 14th November, 2024. This depiction of the square of opposition was created by Gabriel Blanchard with Canva; this post was updated with this image on 19th November, 2024. It was updated again on 4th December, 2024, in ways which did not substantively affect its content.