Sorting Through Sophistries:
The Know-Nothings
—Part II

By Gabriel Blanchard
It is said, and with truth, that numbers don't lie. Unfortunately, this is only because numbers don't speak: people, who are the ones that say numbers, lie very capably.
A Revue of Ignorances
Last time we dipped into our reproaches against the Sophists, we talked about various subtypes of the fallacious appeal to ignorance, beginning with the ad ignorantiam proper (and its connection to shifting the burden of proof). We also covered the false dilemma and the fool’s-golden mean.
Incidentally, one recurring theme of this series has been that of allowing one’s intellectual opponents the benefit of the doubt when it comes to fallacies. Fallacies are wrong in any case, and that is a complete criticism in itself: we do not need to go further and attribute deliberate malice to our opponents (people make mistakes for lots of reasons, and malice is only one of them). Because genuine ignorance is at the root of a great many errors, this courtesy is especially relevant when analyzing the “know-nothing” family; for a slightly different extra reason, it will be important later in this piece.
We must now pass to a subtype that is—unluckily—not only exceedingly common and easy to commit, but also often difficult to detect. Now, some instances are painfully easy to detect; in fact, one of them has become a proverb: correlation does not imply causation. An even more easily detectable type of the same faulty reasoning can be found in the post hoc ergo propter hoc fallacy—the Latin means “after this, therefore because of this,” an error most schoolchildren can spot. Both of these are particular examples of the many fallacies that reach us through the study of probability and statistics.
The Other Agnotology
We have addressed the main meaning of agnotology (the study of ignorance) elsewhere. However, let us pause for a moment to establish a point about the study of probability and statistics—a point where this study intersects with agnotology. It is unlike the rest of statistics, and unlike most other subjects as well. Insofar as statistics measure what has happened, it is a science of demonstrable things. Yet when we use statistical evidence to try to discover trends and chains of causation that impinge on the future, we run into a snag: the future hasn’t happened, and it is therefore not strictly possible to study it.
We all seem to agree in confidently expecting the near future to resemble the near past and other forms of precedent. But we do not know that it will be. We do not know that another instant of time is left to the universe. All studies of probability are measurements, not of how probable things are in themselves, but of their frequency and circumstances in the past, which we then turn round and project onto the future—not because we have any proof that the future must behave according to the same patterns, but because we choose to believe that the cosmos won’t play dirty. The study of probability is thus a study in human ignorance (and one must admit, to be fair, that such thing does invite paradox).
This is hinted at in the calculation of compound probabilities. Even if one starts with a high-probability guess that X will occur, from the moment we begin to try and make guesses further out than that, the likelihood of our prediction of Y plummets, as we pile up layers of ignorance against ourselves.
Those of us with mathematical brains (a category which does not embrace the present author) will doubtless have an easier time grasping the details of these fallacies. In a good many cases, the issue lies in the fact that—whatever the cause in each individual case—certain statistical principles are extremely counter-intuitive. One example is Simpson’s paradox: a trend present in most or all subgroups in a study can vanish, or even be reversed, in the aggregate. That one is, quite frankly, too hard for the present writer; he has instead chosen to make an example of the famous “Monty Hall problem” (named for the host of a game show that featured a puzzle of the type described below).
Exemplum: The Monty Hall Problem
The classic Monty Hall problem features three closed doors. Behind one of them is a new car, while the other two each conceal a goat. A contestant who correctly guesses which door has the car behind it gets to keep the car.
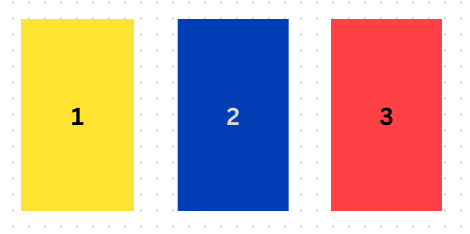
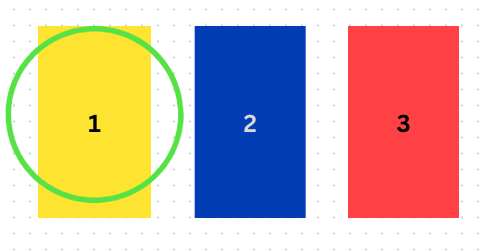
The twist is, the contestant has not one but two guesses. After they make their initial guess (which of course has a 1/3 chance of being correct), one of the doors they did not select is opened, to reveal one of the two goats.

Now. If the contestant—for some strange and personal reason—would rather have a car than a brand-new, ±0.2 horsepower goat, should they stick to their original guess? Or do they have a better chance of getting what they want by switching to the other door (in our example, Door #3)?
Most people’s initial response is that it makes no difference: it’s now a fifty-fifty, surely, so either choice is as good as the other (and most people have at least a mild bias in favor of “staying the course” when all else is equal, and for that matter when it isn’t). However, the truth is that the contestant has a much better chance of winning the car if they change their answer selection from Door #1 to Door #3.

Statistics is the art of stating in precise terms that which one does not know.
William Kruskal, Statistics, Molière, and Henry Adams
Now, here’s why that is the correct answer. The contestant’s chances of picking the door with the car behind it on their first try are only 1/3 (this much is intuitive). The confusing bit is that Door #2 being opened does not change that. The contestant’s odds of having picked the right door with their first guess have not risen to 1/2; they are still only 1/3. It is therefore the best strategy for the contestant to change their guess—and, conveniently, the only logical choice for an alternate guess is Door #3.
It Is Rocket Surgery
Hidden paradoxes like this are a major reason why the misuse of statistics and probability belong among the “know-nothing” fallacies. It is not only easy to use statistics misleadingly: it is easy to do so by accident.
Of course, it is possible to master statistics and to use them to learn. The trouble is simply that it tends to take an amount of work that more or less equates to a master’s degree. For those without an arbitrarily large amount of time to kill, at least one, and ideally both, of two remedies may be used:
- Be highly cautious about any conclusion (particularly in the news** or in the political realm) that professes to be based on statistics. It is an extremely challenging field; the byword of practically all professional statisticians is “thou shalt not jump to conclusions”; and even those people who are trying to use statistics honestly often make elementary mistakes.
- If at all possible, read How to Lie With Statistics by Darrell Huff. Huff was not a mathematician by profession (in fact he was a journalist**), but his introduction to the subject is so effective that How to Lie With Statistics was frequently used as a textbook for many years.
A Butlerian Postscript
The backdrop of statistics casts some valuable light on a recent fad and/or moral panic—one that illustrates certain ways fallacious thinking can impact our daily lives. ChatGPT, and machine learning in general, have been in the news a bit of late, often with predictions (either melancholy or gleeful) that these machine learning tools are going to eliminate entire fields, because we’ll just have the artificial intelligence do that (more on that in a moment).
Put simply, machine learning tools are a kind of pattern recognition software, which runs on statistical principles. Machine learning can be a powerful tool, when applied to the right problem.† However—thanks in no small part to the related, but misleading term “A.I.” (artificial intelligence) that is used for these programs—there is a lot of muddled thinking going around about what machines can and cannot do. The reason calling them “A.I.” is misleading is that intelligence is exactly what these tools don’t have. When we say that they “recognize” patterns, that is a metaphor: these programs are not conscious; they do not have wills or personalities.‡ And this is where we pick up the thread we stowed away near the beginning of this post—the strict distinction between falsehood, which is a fact about an idea in itself, and deceit, which is an intention on the part of a person.
The danger of students using ChatGPT to fake papers and the like is widely recognized. Curiously, there are at the same time many people who think that because these are machines we’re talking about, they are therefore inherently more “objective” or more “fair” than human decision-making could be. After all, it can’t lie—an idea which is plainly inconsistent with the fear, or rather the fact, that it can be used to fake a paper. The real misunderstanding here is (a little ironically) in the word “lie.” Machine learning tools are not capable of conscious malice, which is how we normally define lies. But unluckily, they are perfectly capable of giving you bad information. And that info can be bad in any of a multitude of ways: wrongly defined terms, inadequate or skewed samples, bias in favor of the status quo, you name it. And the reason for all this is perfectly simple: they’re programmed by human beings. That’s where they get everything they have, from design to data set. Machine learning can be a useful tool; what it isn’t is a new brain—or a substitute for one.
*The unclaimed goat is presumably sent into the wilderness to Azazel.
**The issue here is not that journalists are somehow inherently less trustworthy than other people. Their bread and butter lies in weighing sources and their credibility, giving them both the chance to learn some of the basics of statistics, and a strong motive to do so. The problem is that, to be marketable, news has to be “bite-sized,” which means stripping out massive amounts of context; and, as regular readers of this series may recall, context is king.
†Please note that the trolley problem is never the right problem.
‡Pattern recognition is essential to minds as we know them, so machine learning is relevant to artificial intelligence. The problem is, referring to software like ChatGPT as “artificial intelligence” only really makes sense if intelligence is no more than pattern recognition. This is patently false: minds are capable not only of recognizing and rearranging things, but of choosing and intending things, speaking with meaning, and originating things. To confuse acts of that order with pattern recognition is like thinking that if one lavished enough detail and craft on a holographic image, the thing it depicts would become a three-dimensional object.
Gabriel Blanchard has a bachelor’s in Classics from the University of Maryland, and works for CLT as its editor at large. He lives in Baltimore, MD.
Thank you for reading the Journal. If you appreciated this piece and want to learn more about the danger posed to all of us by arithmetic, check out some of our profiles of mathematical and scientific authors, including Archimedes, Avicenna, Sir Isaac Newton, and Albert Einstein; readers who are in a more literary mood might take a look at our introductions to Euripides, Marie de France, William Shakespeare, George Eliot, or Zora Neale Hurston. If you’d like a better grasp of A.I.—even though it doesn’t exist, actually—and what it can and can’t do, Dr. Angela Collier discusses the topic in this video on her YouTube channel (note: occasional adult language); for more reading recommendations, the acclaimed Dr. Cornel West gave us a whole library’s worth a few years back when he appeared on the official CLT podcast, Anchored.
Published on 4th April, 2024. Page image of xkcd 688, “Self-Description”; illustrative images for the Monty Hall problem created via Canva. This post was updated on 5th December 2024, in ways that did not substantively affect its content.