The Brain, a User's Manual:
Using the Square of Opposition

By Gabriel Blanchard
Logic makes us think of the angels—either because angelic minds are said to intuitively see what humans must reason our way to, or because angels must so often say "Fear not."
The Square of Opposition: A Review
Having established what A, I, E, and O statements are, and why it matters, we have now to plug them into the square of opposition—what we described last time as a sort of “logic calculator.”
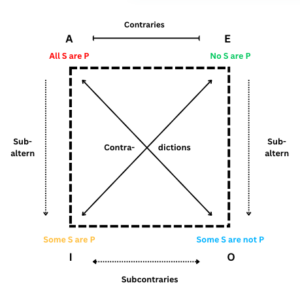
We have alluded to some of the relationships outlined in the diagram above before. (Contradiction obviously comes up a good deal, both directly and indirectly, in any discussion of critical thinking; in our previous series on fallacies, we also touched directly on two misuses of subalternation, the A-I and E-O dynamics.)
Let us now define the four interrelationships on that diagram in more detail. One-sentence summaries stand below each heading, to help you remember how each operation works. (Don’t be alarmed if you don’t understand the summaries at first! The following paragraphs explain each of them: the summaries are only there to help you remember.)
1. Subalternate (the A-I and E-O dynamics)
If the superaltern is true, its subaltern must be true;
but almost nothing can be inferred from a true subaltern by itself.
We should begin with the relation between statements of the same quality (affirmative or negative).1 A misunderstanding occasionally arises here; some beginners suppose that “Some S are P” should be understood to mean “Only some S are P (not all),” or “Only some S are not P (but some are).” That might be the right way to understand a specific speaker, depending on the context; however, it is not what the logical I and O statements mean. Instead, the I and O statements are more like “At least some S are P” and “At least some S are not P.” This is because logic—like a few other branches of reasoning, such as statistics and probability—is much more strict with us than we usually are with ourselves about recognizing when we don’t know something. (In truth, this is where deductive logic gets not only its limitations, but its unrivaled power when used by those who understand its limitations; but we can’t stop for that now.)
So! Statements which have the same quality, affirmative or negative, are one another’s alterns: the universal statements are superalterns; the particular statements, subalterns. If a superaltern is true, its corresponding subaltern must be true, necessarily, without exception. If “No rocks are edible” is true, then any smaller collection of rocks (which, logically, is all “some” means) will also be inedible—more succinctly, if “No rocks are edible,” then “Some rocks are not edible.” This movement from universal to particular is called superalternation, and, because it is, well, brutally obvious, it isn’t of much use …
Except when turned the other way. For of course if an I statement necessarily follows from an A, then, if we can disprove the I statement, we’ve already disproven the A statement; obviously, the same goes for Os and Es too.2 Moving from the falsity of the particular statement to the falsity of its corresponding universal is called subalternation. This is why the arrows from the universals A and E down to the particulars I and O only point in one direction: proof only goes in one direction along this relationship; go the opposite way, and you have disproof.
All men have the same substantial form ... But Thomas is different from Bonaventure, Thomas is fat while Bonaventure is thin, and it may even be that Hugh is bad while Francis is good, and Aldemar is phlegmatic while Agilulf is bilious. Or am I mistaken?
Umberto Eco, The Name of the Rose, Third Day: Nones
2. Contradictory (the A-O and E-I dynamics)
One must be true, and one must be false.
Contradiction is a bit easier! Contradictory statements cannot both be true, and they cannot both be false—unless they involve some sort of category error that keeps them from being true or false in any ordinary sense (but this should ideally be taken care of while defining one’s terms, an earlier step in the reasoning process). Either “No exams take place on Wednesdays,” or “Some exams take place on Wednesdays”: there is no secret third option.
3. Contrary (the A-E dynamic)
Both cannot be true; both can be false.
Here, though, we run into something a little bit subtler. At first glance, it might seem like A and E should be on the list of contradictory statements too. They can’t both be true, can they! No; but they can both be false. If we disprove the claim that “No dogs are brown,” it does not follow that “All dogs are brown.” From knowing that the E statement is false, the law of contradiction only proves that “Some dogs are brown” must be true; there could still be non-brown dogs.
4. Subcontrary (the I-O dynamic)
Both cannot be false; both can be true.
Here, the dynamic is like a “soft” or “inverse” version of the dynamic between the universals. If “Some planets are inhabited,” then it might also be true that they all are; or, it might also turn out that some are not. But at least one particular statement must be true either way.
And that’s the whole square of opposition. Yes, really! We’ve got one more basic topic to review, which is how to build syllogisms (how to build valid, sound syllogisms, to be specific—anybody can build a bad syllogism); with that completed, we will be two-thirds of the way through this crash course in logic!
1As we discussed earlier in this series, “quality” can have many distinct meanings. On the square of opposition, however, it refers to the affirmative and negative qualities specifically; likewise, “quantity” in this context refers to universal and particular quantities. The quality and quantity of each of the four statements is therefore: A, universal affirmative; I, particular affirmative; E, universal negative; O, particular negative.
2This is part of what is meant when people talk about “the difficulty of proving a universal negative.”
Gabriel Blanchard is a graduate of Rockbridge Academy and holds a degree in Classics from the University of Maryland, College Park. He lives in Baltimore, MD.
If you have only just joined us here, but have enjoyed this piece and would like to read The Brain, a User’s Manual from the beginning, prior installments include: our introduction to logic as such; our discussion of the value and technique of definition; our three-part chapter on predication, discussing substances, categories, and non-categorical relations of various sorts; and our explanation of the four kinds of statements (A, I, E, and O) used in the square of opposition. Or if you’d like to change tacks and read about something from the artistic and literary world, why not try our short bios of Virgil, the Pearl poet, John Donne, George Eliot, or Zora Neale Hurston?
Published on 5th December, 2024. Page image of an 18th-century Persian astrolabe, an astronomical device invented in classical antiquity that could be used to identify planets and stars, navigate, and even tell time; photo by Andrew Dunn, used under a CC BY-SA 2.0 license (source). Depiction of the square of opposition by Gabriel Blanchard, created with Canva.